Question

Solve a value mixture problem using a system of linear equation

Answer 1

Let A and B be the number of advance and same-day tickets sold. From the question we can write the following relations:

`\begin{gathered} A+B=70 \\ A*15+B*35=1650 \end{gathered}`

From this, we can isolate A in the first relation and substitute it in the second. This way we can find the value of B, as follows:

`\begin{gathered} A=70-B \\ \\ (70-B)*15+35B=1650\to1050-15B+35B=1650\to \\ \to20B=1650-1050=600\to B=(600)/(20)=30 \end{gathered}`

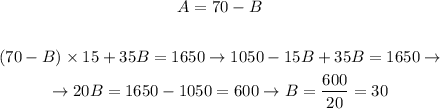
From this, we can substitute the value of B in the first relation to find A.

`A+30=70\to A=70-30=40`

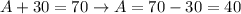
From this, we conclude that:

The number of advance tickets sold is 40

The number of same-day tickets sold is 30