If f is a differentiable function, and x_0 is a critical point (local maximum or minimum), then f ' (x_0)=0.
To find the values of x_0 such that f ' (x_0)=0, differentiate the function:
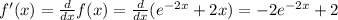
Assume that f ' (x_0)=0:
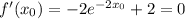
Isolate x_0:
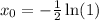
Since the natural logarithm of 1 is 0, then:
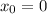
To check whether x_0 is a local maximum or a minimum, find the second derivative of f:
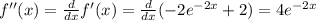
Evaluate f '' (x) at x=0:
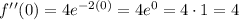
Since f ' (0)=0 and f '' (0)=4>0, then 0 is a local minimum value for the function f.