Question

Hi! I’m not quite sure how to make a graph from polynomial functions. Can you help me figure out how to graph P(x)=(x+10)(x+7)(x-12) without using a calculator & also figure out what degree the graph is?

Answer 1

• Degree: 3

,

• Graph below

Explanation:

Given the function:

`P\left(x\right)=\left(x+10\right)\left(x+7\right)\left(x-12\right)`

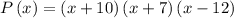
• The roots of the function are -10, -7, and 12.

,

• The function is of degree 3.

When x=0

`\begin{gathered} P(x)=(x+10)(x+7)(x-12) \\ P(0)=(0+10)(0+7)(0-12)=-840 \end{gathered}`

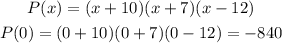
The y-intercept is at (0, -840).

Now, to graph the polynomial, first, find we determine the critical points by finding the derivative of the function.

First, expand P(x)

`\begin{gathered} P(x)=(x+10)(x^2-12x+7x-84) \\ =(x+10)(x^2-5x-84) \\ =x^3-5x^2-84x+10x^2-50x-840 \\ P(x)=x^3+5x^2-134x-840 \end{gathered}`

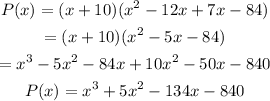
Next, find the derivative:

`P^(\prime)(x)=3x^2+10x-134`

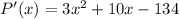
Set the derivative equal to 0 and solve for x:

`\begin{gathered} 3x^2+10x-134=0 \\ \implies x=-8.55,5.22 \end{gathered}`

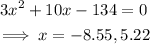
Find the corresponding y values at x=-8.55 and 5.22.

`\begin{gathered} P(x)=(x+10)(x+7)(x-12) \\ P(-8.55)=(-8.55+10)(-8.55+7)(-8.55-12)=46.19 \\ P(5.22)=(5.22+10)(5.22+7)(5.22-12)=-1261.00 \end{gathered}`

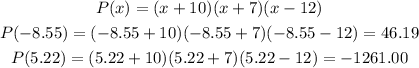
So far, we have the following:

• Roots: (-10, 0), (-7, 0), (12, 0)

,

• The y-intercept is at (0,-840).

,

• Critical Points: (-8.55, 46.19), (5.22, -1261)

A sketch of these points is given below:

You can use this as a better guide: