According to the statement of the problem:
• we know that the ripple travels outward at a speed ,v = 20 cm/s,,
,
• we must compute the spread of the circular ripple after a time ,t = 25 s,, i.e. we must compute the distance travelled by the ripple after that time.
Because the ripple travels at a constant velocity, the distance travelled after the time t, is given by:
![r(t)=v\cdot t=20\frac{\operatorname{cm}}{s}\cdot25s=20\cdot25\operatorname{cm}=500\operatorname{cm}\text{.}]()
The area of the circular ripple in terms of its radius is given by the following formula:

Because the radius is a function of the time, we have that the area is also a function of time:
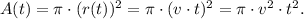
Replacing the values v = 20 cm/s and t = 25 s, we have that:
![A(t)=\pi\cdot(20(cm)/(s)\cdot25s)^2=\pi\cdot(500\operatorname{cm})^2=25000\pi\cdot cm^2\cong785398.16cm^2.]()
Answer
The circular ripple has a radius of 500 cm and its area is 25000π cm² ≅ 785398.16 cm².