Question

A rectangle has a length of 18 yards less than 6 times its width. If the area of the rectangle is 4200 square yards, find the length of the rectangle.

Answer 1

Data

• Length of 18 yards less than 6 times its width.

,

• The area of the rectangle is 4200 square yards.

Procedure

To solve this problem we have to build two equations as we have two unknown variables (the length, and the width).

• Equation 1 - the of a rectangle (Ar) is given by:

`A_r=l* w`

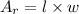
where l is the length and w is the width.

• Equation 2: we can convert "the length is 18 yards less than 6 times its width." into an algebraic expression:

`l=6w-18`

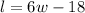
Then, we can replace the Equation 2 in the Equation 1, to get Equation 1 in terms of w:

`A_r=(6w-18)* w`

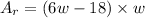
Simplifying the expression:

`A_r=6w^2-18w`

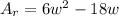
Additionally, we can replace the area of the rectangle as it is given:

`4200=6w^2-18w`

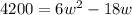
As it is a quadratic equation, we can use the General Quadratic Formula:

`x_(1,2)=(-b\pm√(b^2-4ac))/(2a)`

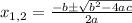
where a, b and c represent the coefficients from the quadratic equation in the form:

`0=ax^2+bx+c`

Then, in order to use the Quadratic Formula, we have to set our quadratic equation to 0:

`0=6w^2-18w-4200`

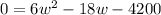
In this case, a = 6, b = -18, and c = -4200. Replacing them in the formula:

`x_(1,2)=(-(-18)\pm√((-18)^2-4(6)(-4200)))/(2(6))`

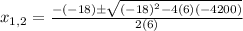
Simplifying the terms inside the square root and the denominator:

`x_(1,2)=(18\pm√(324+100,800))/(12)`
`x_(1,2)=(18\pm√(101124))/(12)`
`x_(1,2)=(18\pm318)/(12)`

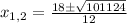
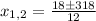
As it is a square root, we obtain two solutions:

`x_1=(18+318)/(12)=28`
`x_2=(18-318)/(12)=-25`

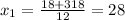
As we cannot have a negative side, then our solution for w is 28.

Then, knowing that w = 28, we can replace this value in Equation 2 and get l:

`l=6(28)-18`
`l=150`

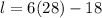
Answer: the length is 150 yards.