Question

here are summary statistics for randomly selected weights of newborn girls n=165 x bar=28.6hg s=6.3hg Construct a confidence interval estimate of the mean. use a 99% confidence level Are these results very different from the confidence interval 26.6 hg < u<29.8 hg with only 17 samples values x bar= 28.2 hg and s = 2.2 hgWhat is the confidence interval for the population mean μ?

Answer 1

For this case we cna use the following formula for the confidence interval:

The degrees of freedom are: df = 165-1= 164

For this case the significance level is 1-0.99 = 0.01 and the value of alpha/2 = 0.005 then the critical value is:

t =2.606

Replacing we have:

`28.6\pm2.606\cdot\frac{6.3}{\sqrt[]{165}}`

Solving we got:

`27.32\le\mu\le29.88`

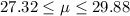
And after round to one decimal we got:

27.3 <= mu <= 29.9