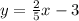To solve the exercise you can first take the equation of the given line to its slope-intercept form, that is,
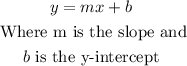
To take the equation of the given line to its slope-intercept form, you can solve for y, like this

Now, two lines are perpendicular if their slopes satisfy the equation
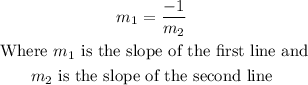
So, in this case, you have
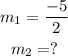

Therefore, the equation that represents a line that is perpendicular to the line 5x + 2y = 12 is