Question

3. A dining hall had a total of 18 tables - some long rectangular tables and some round ones. Long tables canseat 8 people. Round tables can seat 6 people. On a busy evening, all 130 seats at the tables are occupied.Write a system of equations that can be used to determine how many rectangular tables and round tables arebeing used that evening.

Answer 1

We define the following variables:

R = # of rectamgular tables

C = # of circular tables

From the statement we know that we have a total of 18 tables, so the # of rect. tables plus the # of circ. tables must sum 18:

`18=R+C`

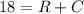
We also know that we have 130 occupied seats, so we can write the following equation in terms of R and C (taking in account that each one can have 8 and 6 persons, respectively):

`130=8\cdot R+6\cdot C`

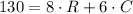
So we must solve the following system of equations:

`\begin{gathered} 18=R+C \\ 130=8R+6C \end{gathered}`

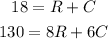
In order to solve the system we can do the following steps: