The work done by a constant force in a rectilinear motion is given by:
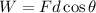
where F is the magnitude of the force, d is the distance and θ is the angle between the force and the displacement vector.
In this case we have two forces then we need to add the work done by each of them; for the first force we have a magnitude of 17 N, a displacement of 12 m and and angle of 0° (since both the displacement and the force point right); for the second force we have a magnitude of 36 N, a displacement of 12 m and an angle of 30°. Plugging these values we have that the total work is:
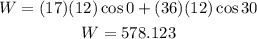
Therefore, the total work done is 578.123 J and the answer is option E