Let us draw a sketch to understand the question
Since A is an acute angle, then it lies on the 1st quadrant
Since B is a reflex angle, then it lies on the 3rd quadrant
In the first quadrant, all ratios are +ve
In the 3rd quadrant sin and cos - ve but the tan is +ve
We will use the identity
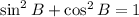
To find the value of sin B because tan B = sin B/cos B
Since cos B = -4/5, then
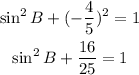
Subtract 16/25 from both sides
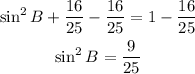
Take a square root for both sides
![\begin{gathered} \sqrt[]{\sin^2B}=\pm\sqrt[]{(9)/(25)} \\ \sin B=-(3)/(5) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/a9yodcg8r2fits1exu0zlg184gxa82lha5.png)
We take the negative value because sin in the 3rd quadrant is -ve
Divide sin B by cos B to find tan B
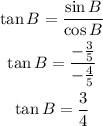
a) tan B = 3/4
Since sin(A + b) = sinA cosB + SinB cosA --------(1)
Then we have to find the value of cos A, we will use the identity above
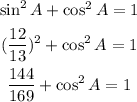
Subtract 144/169 from both sides to find the value of cos^2A
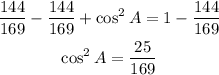
Take a square root for both sides, then
![\begin{gathered} \sqrt[]{\cos^2A}=\pm\sqrt[]{(25)/(169)} \\ \cos A=(5)/(13) \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yhjcqbug6801hyt0rk4qjsbmlmxcd4w1ds.png)
Substitute the values of sin A, cos A, and sin B, cos B in expression (1) above to find sin (A + B)
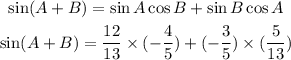
Simplify it

b) sin(A + b) = -63/65