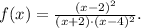We must write an equation for the function in the graph.
From the graph, we see that the function f(x):
0. has a vertical asymptote at x = -2 → f must be proportional to 1/(x + 2),
,
1. has a vertical asymptote at x = 4 → f must be proportional to 1/(x - 4),
,
2. is zero at x = 2 → f must be proportional to (x - 2).
Now, we also see that the function:
• is negative for x < -2,
,
• looks like a parabola in the interval -2 < x < 4 → f is proportional 1/(x + 2)²,
,
• is positive in the interval -2 < x < 4 → f must be proportional 1/(x - 4)² to have a positive sign for values x < 4.
Taking into consideration all the points above, we write the following function:
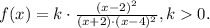
Where k is a positive constant.
Selecting the value k = 1 and plotting the function f(x), we get the following graph:
Answer
An equation for the function in the graph is: