Hello there. To solve this question, we'll have to remember some properties about the sum-to-product formula.
Given the trigonometric expression:

We have to simplify it.
First, remember the angle sum formulas:
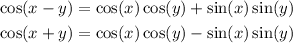
Subtracting the second equation from the second equation, we'll have:
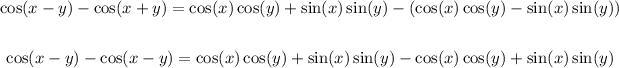
Add the terms
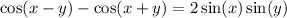
This is also known as one of the sum-to-product formulas;