Question

Find: when does the object move away and when towards the starting point?Given:

Answer 1

• Away from the starting point: (0, 5) U (7, 20)

,

• Towards the starting point: (5, 7)

Step-by-step explanation

If the function s(t) represents the distance from the starting point to the object, then as this function increases the distance increases. Similarly, as the function decreases, the distance also decreases. This means that the object is moving away from the starting point when the function is increasing - as long as it is positive, and towards the starting point when the function is decreasing.

In this function, there is a zero at t = 0 and at t = 7. The first zero is at the starting point and the second zero is when the object reaches back to the starting point. Between these two zeros, there is a maximum value that we can find using the derivative of the position function. To find the derivative, apply the distributive property first,

`s(t)=7t^(5/2)-t^(5/2)t=7t^(5/2)-t^(7/2)`

Find the derivative,

`s^(\prime)(t)=7\cdot(5)/(2)\cdot t^(5/2-1)-(7)/(2)\cdot t^(7/2-1)=(35)/(2)t^(3/2)-(7)/(2)t^(5/2)`

Factor our 7/2 t ^(3/2),

`s^(\prime)(t)=(7)/(2)t^(3/2)(5-t)`

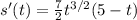
The maximum (or minimum) is where the derivative is equal to zero, and this happens at t = 0 and at t = 5. Hence, the object changes direction at t = 5.

Also, the object crosses the starting point at t = 7, and then it goes on infinitely. But since t is between 0 and 20, we can say that it stops at t = 20.

Hence, the object moves away from the starting point in the interval (0, 5), then towards the starting point in the interval (5, 7), and finally, away from the starting point in the interval (7, 20).