Question

Tom has 7 more dollars than Jimi. together they have a total of 71 Silver dollars. how many silver dollars does Tom have?

Answer 1

Let's say Tom has T silver dollars, and Jimi has J silver dollars.

If tom has 7 more dollars than Jimi, then we can express it as follows:

`T=J+7`

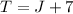
The total amount they both have is 77, then, it can be expressed as follows:

`T+J=71`

Now we have a system of two equations and two unknowns.

An easy way to solve this is replacing the first equation in the second:

`J+7+J=71`

Then, operating:

`2J+7=71`

Now, solving for J:

`\begin{gathered} 2J=71-7 \\ 2J=64 \\ J=(64)/(2) \\ J=32 \end{gathered}`

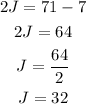
Now we have found how many silver dollars Jimi has. We can now use again the first equation we stated, replacing 32 where we have J:

`\begin{gathered} T=J+7 \\ T=32+7 \\ T=39 \end{gathered}`

Then, Tom has 39 silver dollars.

We can prove this because 39 is 7 more than 32, and 39 + 32 = 71