The given function is,
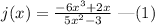
To find j(0), substitute x=0 in expression (1).
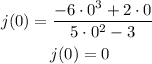
So, j(0)=0.
To find j(2), substitute x=2 in expression (1).
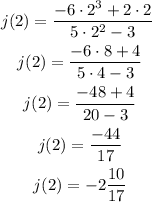
Therefore, j(2)=-2 10/17.
To find j(-2), substitute x=-2 in expression (1).
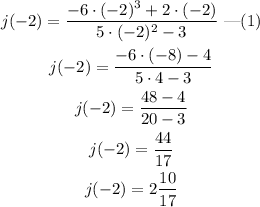
Therefore, j(-2)=2 10/17.
So, the obtained values are,
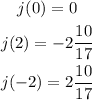
Comparing the values of j(0), j(2) and j(-2), we get
j(2)
Therefore, the statement j(-2)> j(0) is correct.