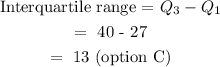Question

Use the data below for questions 1-4. The ag 33, 25, 42, 25, 31, 37, 46, 29, 38 show 1. What is the first quartile of the data? A. 25 5. B. 27 C. 29 D. 33 2. What is the third quartile of the data? A. 37 B. 38 C. 40

Answer 1

First, we re-arrange the data in ascending order

`25,\text{ 25, 29, 31, 33, 37, 38, 42, 46}`

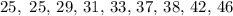
To obtain the first quartile, we use the formula:

`Q_1\text{ = }(1)/(4)\text{ (n + 1) th}`

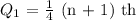
n is the total number of values, which is 9

`\begin{gathered} Q_1\text{ = }(1)/(4)\text{ }*\text{ (9 + 1)} \\ =\text{ 2.5 th} \end{gathered}`

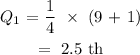
Checking through the data, this corresponds to 25 and 29. We take the average

`\begin{gathered} Q_1\text{ = }\frac{25\text{ + 29}}{2} \\ =\text{ 27 (option B)} \end{gathered}`

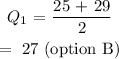
Similarly, to obtain the third quartile, we use the formula:

`Q_3\text{ = }(3)/(4)\text{ }*\text{ (n + 1)}`

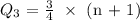
Therefore:

`\begin{gathered} \text{Position of Q}_3\text{ = }(3)/(4)\text{ }*\text{ (9 + 1)} \\ =\text{ 7.5 th} \end{gathered}`

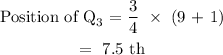
Checking through the data, this corresponds to 38 and 42, so we take the average

`\begin{gathered} Q_3\text{ = }\frac{38\text{ + 42}}{2} \\ =\text{ 40 (option C)} \end{gathered}`

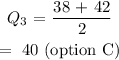
Formula for interquartile range:

`\begin{gathered} \text{Interquartile range = }Q_3-Q_1 \\ =\text{ }40\text{ - 27} \\ =\text{ 13 (option C)} \end{gathered}`