Question

How many and what type of solution(s) does the equation have?8p^2 = 24p - 10

Answer 1

In order to find the number and type of solutions, let's calculate the value of the discriminant Delta in the quadratic formula:

`\begin{gathered} 8p^2=24p-10 \\ 8p^2-24p+10=0 \\ 4p^2-12p+5=0 \\ \\ a=4,b=-12,c=5 \\ \Delta=b^2-4ac \\ \Delta=(-12)^2-4\cdot4\cdot5 \\ \Delta=144-80 \\ \Delta=64 \end{gathered}`

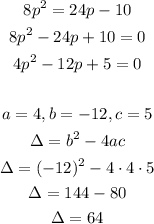
Now, let's calculate the solutions of the equation:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{\Delta}}{2a} \\ x_1=(12+8)/(8)=(20)/(8)=2.5 \\ x_2=(12-8)/(8)=(4)/(8)=0.5 \end{gathered}`

We have two rational solutions, therefore the correct option is the fourth one.