The length of the room is l
since the length of the room is three times the width w so,
l=3w
The expression for the perimeter of rectangle is
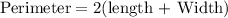
Since perimetr is greater than the 120,

Inequality to represnt the statement the length, 1, of a rectangular room is three times its width, w is
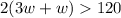
solve for w,
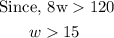
Thus, the value of w must be greater than 15.