Question

John recently drove to visit his parents who live 750 miles away. On his way there his average speed was 11 miles per hours faster than on his way home. If John spent a total of 25 hours driving, find the two rates in miles per hour. Round your answer to two decimal places, if needed

Answer 1

The average speed when John was going to his parents house times the amount of time he took to drive must be equal to the distance. The same is true for the path back home. If we call the amount of time he took to drive to his parents house as t1, the time he took to drive back as t2, and the average speed on the way back as x, we have the following equations:

`\begin{gathered} (x+11)t_1=750 \\ xt_2=750 \\ t_1+t_2=25 \end{gathered}`

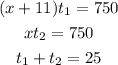
If we solve the first two equations for the times t1 and t2, we're going to have:

`\begin{gathered} t_1=(750)/(x+11) \\ t_2=(750)/(x) \end{gathered}`

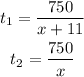
Then, if we substitute those expressions on the third equation, we have:

`(750)/(x+11)+(750)/(x)=25`

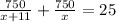
Solving for x:

`\begin{gathered} (750)/(x+11)+(750)/(x)=25 \\ \\ (750x)/(x+11)+750=25x \\ 750x+750(x+11)=25x(x+11) \\ 1500x+8250=25x(x+11) \\ 60x+330=x(x+11) \\ 60x+330=x^2+11x \\ 49x+330=x^2 \\ -x^2+49x+330=0 \end{gathered}`

Using the quadratic equation, the solution for this expression is:

`\begin{gathered} x_(\pm)=(-(49)\pm√((49)^2-4(-1)(330)))/(2(-1)) \\ =(-49\pm61)/(-2) \\ =(49+61)/(2) \\ =(110)/(2) \\ =55 \end{gathered}`

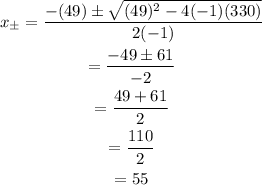
Then, John average speed going to his parents house was 66 mph while the average speed coming back was 55 mph.