Hello there. To solve this question, we'll have to remember some properties about coordinate geometry.
Given the following rectangle in the coordinate plane:
First, we determine the coordinates of the vertices A, B, C and D.
Notice that we can calculate its dimensions by simply calculating the distance between each vertex.
In this case, since we have a rectangle, the sides are pairwise congruent, which means that AB // DC and AD // BC and have the same measures.
The distance formula d(x,y) for two points (x0, y0) and (x1, y1) is given by:
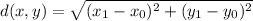
As suggested, we only have to measure two sides of it, hence choosing the sides AB and AD, we'll get
Determining the coordinates of A: it is the point (-4,4)
Determining the coordinates of B: it is the point (10, 4)
Determining the coordinates of D: it is the point (-4, -4)
Using the distance formula, we get
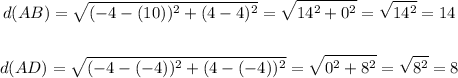
Hence, we got
Its dimensions are given by
mAB x mAD = 14 units x 8 units.
This is the answer to this question and it is contained in the last option.