Question

Round to the nearest 4 decimal places. Directions in pic

Answer 1

a)

From a standard normal distribution table we have that:

`P(z>1.3)=0.0968`

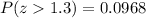
b)

In this case we need to use the z-score defined as:

`z=(x-\mu)/(\sigma)`

where mu is the mean, sigma is the standard deviation and x is the value we are looking for; in this case we would have:

`\begin{gathered} P(X<85)=P(z<(85-89)/(11)) \\ =P(z<-0.3636) \\ =0.3581 \end{gathered}`

Therefore:

`P(X<85)=0.3581`

c)

Using the method in the previous part and the probability properties we have:

Therefore approximately 25 teams have at least 76 points.