Let there be 'n' persons at the party.
Since each person shakes hand with every other person exactly once, the total number of handshakes will be the number of ways of selecting two person from the party.
Consider that the number of ways of selecting 'r' objects from 'n' distinct objects is given by,
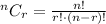
So the number of ways of selecting 2 from 'n' people at the party will be,
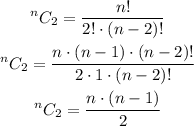
Given that the total number of handshakes is 66,

Solve the above quadratic equation using the quadratic formula,
![undefined]()