A logistic growth model for the world population is:
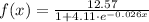
Where x is the number of years since 1958 and f(x) is expressed in billions
It's required to find the year for which the world population will be f(x) = 9 billion.
Then we set up the equation:
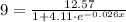
Cross-multiplying:

Dividing by 9:
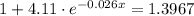
Subtracting 1 and dividing by 4.11:
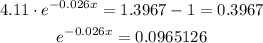
Taking logarithms on both sides:
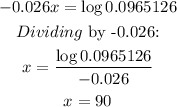
According to this model, the world population will be 9 billion in 90 years from 1958, that is, in the year 2048