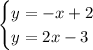From the first table, we can use the points (-1,3) and (5,-3) to find the first equation:
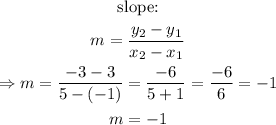
then we can use the point to find the equation in slope-point form:
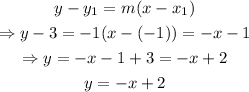
we can do the same with the next table, using the points (1,-1) and (7,11):
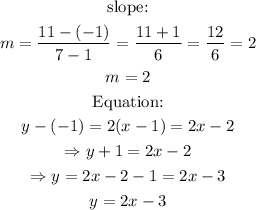
therefore, the system of equations is: