Solution
- The eccentricity of an ellipse is given below:
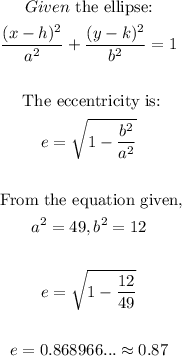
- The eccentricity is 0.87
- Because the eccentricity is close to 1, it means it is flatter than normal. Thus, it is "elongated then circular"
Final Answer
- The eccentricity is 0.87
- "elongated then circular"