Question

QuestionThe data set below contains the average low temperatures in April for 9 Alaskan cities. What is the interquartile range ofthis data set?5, 12, 14, 19, 19, 21, 25, 29, 33

Answer 1

Answer:

Interquartile range = 14

Explanations:

The given data set is:

5, 12, 14, 19, 19, 21, 25, 29, 33

Find the median (Q₂) of the data set:

Q₂ = 19

Divide the data set into two:

The lower half of the data set is 5, 12, 14, 19

The lower quartile (Q₁) is the median of the lower half of the data set

`\begin{gathered} Q_1=\text{ }(12+14)/(2) \\ Q_1=\text{ }(26)/(2) \\ Q_1=\text{ 13} \end{gathered}`

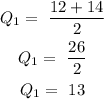
The upper half of the data set is: 21, 25, 29, 33

The upper quartile (Q₃) is the median of the upper half of the data set

`\begin{gathered} Q_3\text{ = }(25+29)/(2) \\ Q_3\text{ = }(54)/(2) \\ Q_3=\text{ 27} \end{gathered}`

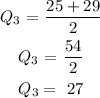
The interquartile range ( IQR) is the difference between the upper quartile and the lower quartile

IQR = Q₃ - Q₁

IQR = 27 - 13

IQR = 14