Question

miles per hour. Charlie left 1 hour later, biking at a rate of 20 miles per hour. How long will it take Charlie to catch up to Bernie?

Answer 1

Let t be the number of hours it takes Charlie to catch up with Bernie.

`\begin{gathered} \text{Speed}=\frac{dis\tan ce}{\text{time}} \\ \text{distance}=\text{speed}* time \end{gathered}`

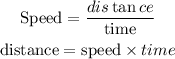
Given:

For Charlie

time = t

speed = 20mph

`\begin{gathered} \text{Charlie's distance covered = sp}eed\text{ x time} \\ Charlie^(\prime)sdistance=20\text{ x t } \\ =20t\text{ miles} \end{gathered}`

For Bernie, he has started 1 hour earlier

Given:

time = t + 1

speed = 15mph

`\begin{gathered} \text{Bernie's distance covered will be;} \\ \text{speed x time = 15(t+1)} \\ =15t+15\text{ miles} \end{gathered}`

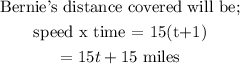
Hence, to get the time it will take for Charlie to catch up, we equate the distance both of them covered

`\begin{gathered} 15t+15=20t \\ \text{Collecting the like terms,} \\ 15=20t-15t \\ 15=5t \\ \text{Dividing both sides by 5,} \\ t=(15)/(5) \\ t=3\text{hours} \end{gathered}`

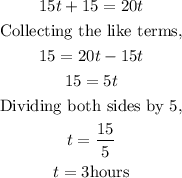
Therefore, it will take Charlie 3hours to catch up with Bernie.