Question

X^4-3x^3-1,000 / x+5. It is x to the 4th power - 3x to the third power - 1,000 all divided by x+5 And we need to divide it using the long division method.

Answer 1

We have the following polynomial division:

`(x^4-3x^3-1000)/(x+5)`

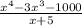
And we need to use the long division method to solve it.

To perform the long division method, we have to proceed as follows:

1. We can rewrite the division as follows:

2. Now, we have to divide the first term of the polynomial x^4 by the first term of the divisor to obtain the first term of the quotient:

`(x^4)/(x)=x^3`

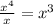
3. This is the first term of the quotient. Then we have to multiply it by the divisor, and change the sign of the result since we have to subtract it from the terms of the dividend:

4. Now, we have to repeat the process with -8x^3 as follows:

`-(8x^3)/(x)=-8x^2`

This is the second term of the quotient.

5. Then we have:

6. Now, we have to divide 40x^2 by x:

`(40x^2)/(x)=40x`

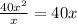
This is the third term of the quotient. Then we have:

7. Now, we have to divide -200x by x again, and then we have:

`-(200x)/(x)=-200`

And now we have:

Therefore, in summary, we have that the q