Question

12. Four cupids-to-be arrived recently at the Training Center. They need to be assigned to a numbered locker. If there are 18 empty lockers, in how many ways can the 4 cupids be assigned to a locker?formula: nCr=n!/((n-r)!r!))

Answer 1

We are given a combinatorics problem were we need to find in how many ways 4 cupids can be assigned to 18 empty lockers, this is symbolized as:

`C(n,r)`

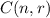
Where "n" is the number of objects, in this case, 18 empty lockers, and "r" is the number of cupids. the formula to find this number is the following:

`C(n,r)=(n!)/(r!(n-r)!)`

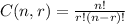
Replacing the known values we get:

`C(18,4)=(18!)/(4!(18-4)!)`

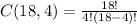
Simplifying:

`C(18,4)=(18!)/(4!(14!))`

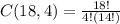
Solving we get:

`C(18,4)=(1\cdot2\cdot3\cdot4\cdot5\cdot6\ldots\ldots18)/((1\cdot2\cdot3\cdot4)(1\cdot2\cdot3\cdot4\ldots.14))`
`C(18,4)=3060`

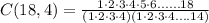
therefore, there are 3060 ways 4 cupids can be assigned to 18 lockers.