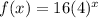Question

Enter an equation for the function that includes the points. Give your answer in the form a (bx). In theevent that a = 1, give your answer in the form bx(-2,4) and (-1,8)The equation is f(x)=

Answer 1

You have the following expression for an exponential function:

`f(x)=a(b)^x`

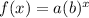
By using the given points (-2,4) and (-1,8), you can find the values of coeffcients a and b, as follow:

The first pair (-2,4) means that for x=-2, f(x)=4:

`4=a(b)^(-2)`

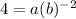
and the second pair (-1,8) means that for x=-1, f(x)=8:

`8=a(b)^(-1)`

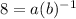
If you divide the second equation between the first equation, you can cancel out coefficient a and solve for b:

`\begin{gathered} (8)/(4)=(a(b)^(-1))/(a(b)^(-2)) \\ 2=(b)^(-1)(b)^2 \\ 2=(b)^(-1+2) \\ 2=b \end{gathered}`

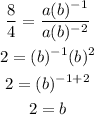
where you have used properties of exponents.

Now, if you replace the previous value of b into any of the equations for the pairs, for instance, into the first equation, you obtain for a:

`\begin{gathered} 4=a(2)^(-2) \\ 4=(a)/((2)^2) \\ 4=(a)/(4) \\ 16=a \end{gathered}`

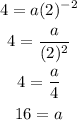
Hence, the form of the function f(x) is:

`f(x)=16(4)^x`