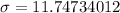d.
The standard deviation for a data set is given by the next formula:
![\sigma=\sqrt[]{\frac{\Sigma(x-x^-)^2_{}}{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/xg7tglgso33n2metdobcdv61wz0pyh69wy.png)
Where n represents the number of data points and x⁻ represents the mean.
Let's check the mean:
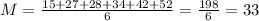
Hence, the mean is 33.
Now, the table for part b:
Where the third column represents the subtraction between x and the means. Also, the fourth column represents the (x-mean)^2.
Where the sum is equal to 828.
Now, we can replace the given values on the standard deviation:
![\sigma=\sqrt[]{\frac{\Sigma(x-x^-)^2_{}}{n}}](https://img.qammunity.org/2023/formulas/mathematics/college/xg7tglgso33n2metdobcdv61wz0pyh69wy.png)
Where the sum (x-mean)^2. = 828 and n = 6( total number of data points)
![\sigma=\sqrt[]{\frac{828^{}_{}}{6}}](https://img.qammunity.org/2023/formulas/mathematics/college/li5hztv0i42h3wq2412vz4za1l634xvzqk.png)
Hence, the standard deviation is given by: