Question

I just need to solve problems C and E. Please explain the question.

Answer 1

C)

We were given that the line of best fit is:

`y=-0.0001x+0.521`

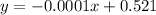
The equation of a straight line is given by the expression:

`\begin{gathered} y=mx+b \\ where\colon \\ m=slope \\ b=y-intercept \end{gathered}`

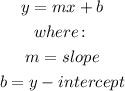
When we compare the equation of the line of best fit with the equation of a straight line, we have:

`\begin{gathered} mx=-0.0001x \\ \text{Divide both sides by ''x'', we have:} \\ slope,m=-0.0001 \\ \\ \therefore slope,m=-0.0001 \end{gathered}`

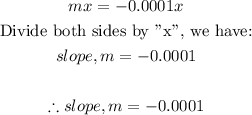
The slope being -0.0001 implies that as the years go by, the winning time keeps reducing at an average rate of 0.0001 seconds per year

D)

Based on the line of best fit, the value of ''r'' (regression coefficient) is close to zero.

A regression coefficient close to zero indicates a weak or no association between the variables

E)

Assuming we choose a value of interest for the years, we have:

`\begin{gathered} 2010\colon t_(2010)=5\colon34\colon05 \\ 2005\colon t_(2005)=\text{?} \\ t_(2005)=5\colon34\colon05+(2)/(5)(5\colon36\colon58-5\colon34\colon05) \\ t_(2005)=5\colon34\colon05+(2)/(5)(2\colon53) \\ t_(2005)=5\colon34\colon05+1\colon09 \\ t_(2005)=5\colon35\colon14 \\ \\ \therefore t_(2005)=5\colon35\colon14 \end{gathered}`

Predicting using the line of best fit;

in the year 2010, the winning time was 5:34:05 seconds

in the year 2005, the winning time was 5:35:14 seconds