Question

Find an equation of variation in which y varies directly as x and y=4 when x=24. Then find the value of y when x=120

Answer 1

Given: y varies directly as x

This can be expressed as:

`y\alpha x`

If we now introduce the constant of proportionality

`y=kx`

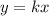
Next, is to find the constant of proportionality

`k=(y)/(x)`

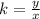
since we have y=4 when x=24, then

`\begin{gathered} k=(4)/(24)=(1)/(6) \\ \\ k=(1)/(6) \end{gathered}`

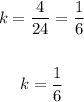
Thus, if we plug in the value of k, we will have the equation of the variation to be:

`y=(1)/(6)x`

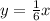
Finally, to get the value of y when x=120, we will simply put x=120 into the formula

so that

`\begin{gathered} y=(1)/(6)*120=20 \\ \\ y=20 \end{gathered}`

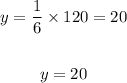
Hence, y = 20