Question

Really need help solving thisThis is from my ACT prep guide to

Answer 1

The sketch above shows the situation described in the exercise.

Knowing the angles of elevation and depression from Neta's point of view and the horizontal distance between both buildings, you can determine the height of the building by using trigonometric ratios.

In both cases, the horizontal distance to the building, the line of vision (to the top or to the bottom), and the vertical height of the building form a right triangle. Where the horizontal distance is the adjacent side to the known angles and the vertical distance is the opposite side, using the tangent you can determine the length of both opposite sides:

Let's start with the upper triangle:

`\begin{gathered} \tan \theta=(opposite)/(adjacent) \\ \tan 56º=(x)/(150) \end{gathered}`

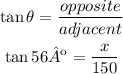
Multiply both sides by 150 to determine the value of x:

`\begin{gathered} 150\cdot\tan 56º=150\cdot(x)/(150) \\ x=222.38ft \end{gathered}`

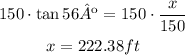
Next, using the lower triangle, calculate the length of the lower portion of the building:

Use the tangent to determine the length of the opposite side "y"

`\begin{gathered} \tan \theta=(opposite)/(adjacent) \\ \tan 32º=(y)/(150) \end{gathered}`

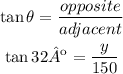
Multiply both sides by 150

`\begin{gathered} 150\cdot\tan 32º=150\cdot(y)/(150) \\ y=93.73 \\ \end{gathered}`

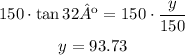
Finally, to determine the height of the neighbor building you have to add both portions:

`x+y=222.38+93.73=316.11\cong316.1ft`

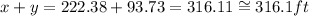
The neighbor building is 316.1ft tall.