The given system of the linear equation has one solution, let's find it.
First, we take equations 1 and 2 and form a system with them to eliminate just one variable.
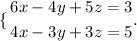
We multiple the second equation by -5/3 to eliminate z,
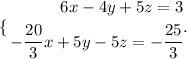
We sum the equations to get one equation with variables x and y

At this point, we have one equation with two variables only. Now, we have to find another equation with two variables only.
So, we repeat the process with the second and the third equation of the given system.
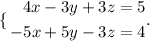
We just have to sum the equations since the variable z can be eliminated by doing that

We now have a second equation with two variables only. Next, we form a new system the new equations we found.
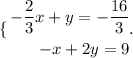
We solve this system to find the values for x and y.
If we multiply the first equation by -2, we would be able to eliminate variable y from the system to find x
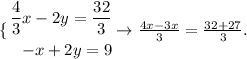
We solve the resulting equation to find x
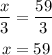
Therefore, the value of x is 59.
Now, we find y
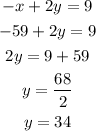
Therefore, the value of y is 34.
At last, we use these two values to find z, we have to use one equation from the initial system.
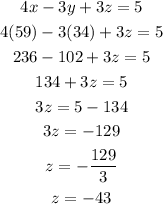
Therefore, the value of z is -43.