Given data:
It is clear from the given image that the triangle is a right angle triangle.
Right angle is at
In a triangle right angle is at C so the hypotenues is always opposite to the right angle that is AB.
Finding the angle B, use trigonometric identity
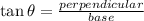
Here, perpendicular is AC because it is always opposite to the angle which we need to find.
AC = 9
Base, BC = 10
Therefore , we have
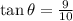
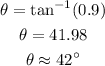
Thus, the correct option is (A) that is 42 degreeD