Part A
The angular speed ω of the carousel equals the ratio between the angle θ that it rotates over the time t that it takes for the carousel to rotate that angle:
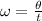
To find the time that it takes for the carousel to rotate two full turns, isolate t from the equation:
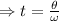
Replace θ=2rev (since 1rev is equal to one turn) and ω=0.11 rev/s:
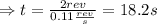
Part B
The circumference of a circle with radius r is equal to 2πr.
To find the tangential velocity of the child (how fast is the child actually moving through space), divide the distance that the child travels over the time that it takes to travel that distance:
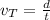
In this case, it takes 18.2 seconds to complete two turns. During that time, the child travels a distance equal to twice the circumference of a circle with radius 3.8m. Find the circumference of a circle with radius 3.8m and then multiply it by 2 to find the total distance that the child traveled:
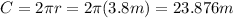
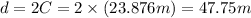
Replace d=47.75m and t=18.2s to find the tangential velocity of the child:
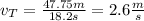
Therefore, the answers are:
a) It takes 18 seconds to go around twice.
b) The child on the horse is traveling at a speed of 2.6 m/s.