Question

Which expression shows the factors of 9x squared plus 3x - 2

Answer 1

`9x^2+3x-2`

we use quadratic formula to find the roots

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

where a is 9, b is 3 and c is -2

replacing

`\begin{gathered} x=\frac{-(3)\pm\sqrt[]{(3)^2-4(9)(-2)}}{2(9)} \\ \\ x=\frac{-3\pm\sqrt[]{9+72}}{18} \\ \\ x=\frac{-3\pm\sqrt[]{81}}{18} \\ \\ x=(-3\pm9)/(18) \end{gathered}`

then x has two values

`\begin{gathered} x_1=(-3+9)/(18)=(1)/(3) \\ \\ x_2=(-3-9)/(18)=-(2)/(3) \end{gathered}`

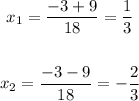
Therea area the roots, values when are replaced the solution is 0 then we can write the factors with this numebrs but opposite sign

then

`(x-(1)/(3))(x+(2)/(3))`

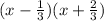
to simplify we can multiply each term by 3, to remove the fractions

`(3x-1)(3x+2)`

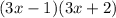
we can invert the position to compare with third option

`(3x+2)(3x-1)`

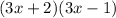
then right option is C