Question

Por Phot blocks 1-1/4-3/4 2. A single card is chosen at random from a standard deck of 52 playing cards, find the following: what is the probability of choosing a card that is not a queen of club? a) P(not a queen of club) b) P(not a red card) c)P (not a face card) d) P(not a heart)

Answer 1

We are asked to find the probability of not choosing a queen of clubs taken at random from a deck of 52 cards. To do that we need to use the following formula.

`P(notquenofclubs)=1-P(Queenofclubs)\text{ }`

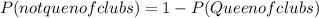
This means that the probability of not choosing a queen of clubs equals one minus the probability of choosing a queen of clubs. Therefore, we have to calculate the probability of getting a queen of clubs first. To do that, let's remember that there are 4 possible queens of clubs in the deck, therefore, the probability of getting one is:

`P(\text{queenofclubs)}=(4)/(52)`

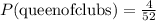
Now we replace that in the formula:

`P(\text{notqueenof clubs)=1-}(4)/(52)`

Solving the operation we get:

`P(\text{notqueenofclubs)=}(12)/(13)`

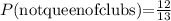
the probability of not getting a queen of clubs is 12/13

From this explanation, you can do the others, remember that this answer will be available in your profile