Given:
Endpoints of the line segment
(-4,3) and (8,9).
Required:
equation for the perpendicular bisector of the line segment
Solution:
First, we have to know the equation of the line segment using the two-point form:
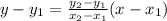
P1 (-4,3) and P2 (8,9).
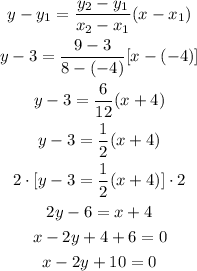
Then, we calculate for the midpoint of the line segment. The formula for the midpoint M( xm,ym ) is:
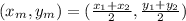
Using P1 (-4,3) and P2 (8,9), the coordintes of the midpoint are
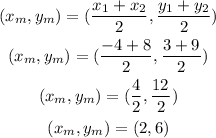
The bisector divides the line segment into two equal parts ( it intersects the line at the midpoint. It is perpendicular to the line segment.
We know that perpendicular lines have opposite-reciprocal slopes.
The slope of the line segment is :
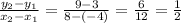
Thus, the slope of the perpendicular bisector is the negative reciprocal of 1/2
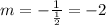
At this point we can now determine the equation of the bisector using the midpoint and the slope of the perpendicular bisector
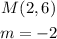
The point-slope form a line is:
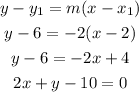
Answer:
The equation of the perpendicular bisector is 2x + y - 10 = 0