In order to determine the sped of Betty at the lowest position, proceed as follow:
The potential energy for a height of 1.22m is:
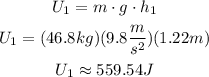
The potential energy at the lowest point is:

Consider that at the starting point all the mechanical energy is potential energy (559.54J). Moreover, when Betty moves through the lowest point, part of the mechanical energy becomes thermal energy and kinetic energy.
Take into account that the for the lowest point, the sum of thermal energy, kinetic energy and potential energy must be equal to the total mechanical energy:
U2 + K + Th = 559.54J
where K is the kinetic energy and Th is the thermal energy. Consider that
Th = 179J
U2 = 191.25J
Solve the equation for K and replace the values of the other contributions to the total energy:
K = 559.54J - U2 - Th
K = 559.54J - 191.25J - 179J
K = 189.29J
Next, take into account that the kinetic energy is given by:
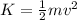
solve the previous equation for v and replace the values of K and m:
![\begin{gathered} v=\sqrt[\square]{(2K)/(m)} \\ v=\sqrt[]{\frac{2(189.29J)}{46.8\operatorname{kg}}} \\ v\approx2.84(m)/(s) \end{gathered}]()
Hence, Betty moves with a speed of approximately 2.84m/s through the lowest point.