Question

What’s the average speed 1st flight 9feet 2nd flight6feet 3rd flight14feetAverage distance airplane +paperclip1st 4feet2nd 6 feet3rd 4 feet Analyze Results:

Answer 1

To calculate the average value of a given set, you have to add all observations and divide it by the number of components of said set.

Using the formula

`(\Sigma x)/(n)`

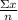
∑x: represents the sum of observations

n= total number of components in the set.

For the first set you have three different observations of three different flights, the average for this set is:

`\begin{gathered} \Sigma x=9+6+14=29 \\ (\Sigma x)/(n)=(29)/(3)=9.67f\exponentialE et \end{gathered}`

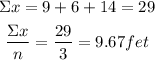
The average distance was 9.67feet

For the second set, you have three observations:

`\begin{gathered} \Sigma x=4+6+4=14 \\ (\Sigma x)/(n)=(14)/(3)=4.67f\exponentialE et \end{gathered}`

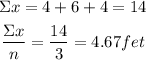
The average distance was 4.67feet

Since theThe airplane flew on average a greater distance in the first time than in the second time.