Given that the principal (P) is $8,788, time (T) is 4 years.
Let R be the annual rate of interest.
Given that the compounding is done 6 times a year, then the rate of interest per period and the number of periods is calculated as,
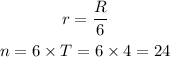
Consider the formula for amount (A) as,
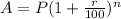
Substitute the values and simplify,

Thus, the annual interest rate of the account is 6.74% approximately.