Question

If lines l, m, and n are parallel, and AB = 2, AC = 8, and EF = 5, what is the length of DE?

Answer 1

Consider the theorem that when a pair of transversals intersect more than two parallel lines, then the ratio of the corresponding segments are always equal.

According to the given problem,

`\begin{gathered} AB=2 \\ AC=8 \\ EF=5 \end{gathered}`

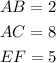
In the given figure, lines ABC and DEF intersect the set of parallel lines 'l', 'm', and 'n'.

Applying the above theorem,

`(AB)/(AC)=(DE)/(DF)`

The expression can be resolved as,

`(AB)/(AC)=(DE)/(DE+EF)`

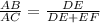
Substitute the values,

`\begin{gathered} (2)/(8)=(DE)/(DE+5) \\ (1)/(4)=(DE)/(DE+5) \end{gathered}`

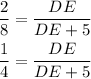
Transpose the terms to simplify,

`\begin{gathered} DE+5=4\cdot DE \\ 4DE-DE=5 \\ 3DE=5 \\ DE=(5)/(3) \end{gathered}`

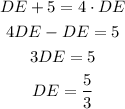
Thus, the value of the segment DE is 5/3 units.