Question

The length of a rectangle is 23 centimeters less than five times its width. it’s an area is 42 square centimeters. Find the dimensions of the rectangle The width is ?And the length is ?

Answer 1

Given:

The length of a rectangle is 23 centimeters less than five times its width.

Let the width of the rectangle = x

So, the length of the rectangle = 5x - 23

The area of the rectangle (A) = Length times Width

And given Area = 42 square centimeters

so,

`\begin{gathered} A=x(5x-23)=42 \\ x(5x-23)=42 \end{gathered}`

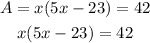
Solve the equation to find x:

`\begin{gathered} x(5x-23)=42^{} \\ 5x^2-23x=42 \\ 5x^2-23x-42=0 \\ (x-6)(5x+7)=0 \\ x-6=0\rightarrow x=6 \\ 5x+7=0\rightarrow x=-(7)/(5)=-1.4 \end{gathered}`

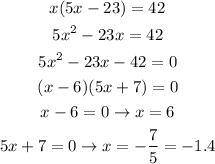
The negative result will be rejected

so, x = 6

So, the width of the rectangle = 6 cm

And the length of the ractangle = 7 cm