Question

AcellusFind the area of the shaded region.Round to the nearest tenth.11.1 m130°Area = [ ? ]m?

Answer 1

294.5 square meters.

Step-by-step explanation:

The shaded region comprises of a sector and a triangle.

`\begin{gathered} \text{Area}=\text{Area of sector+Area of Triangle} \\ =((\theta)/(360\degree)*\pi r^2)+((1)/(2)r^2\sin \alpha) \end{gathered}`

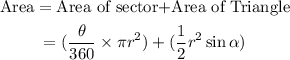
The central angle of the major sector,θ = 360 - 130 = 230 degrees

Therefore:

`\begin{gathered} A=((230\degree)/(360\degree)*\pi*11.1^2)+((1)/(2)*11.1^2*\sin 130\degree) \\ =247.298+47.192 \\ =294.49 \\ \approx294.5m^2 \end{gathered}`

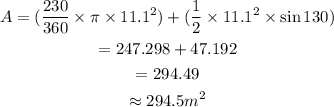
The area of the shaded region is 294.5 square meters (to the nearest tenth).