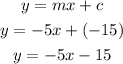Question

How to solve this and get the equation of a perpendicular line and and equation of a parallel line

Answer 1

(a) If two line are perpendicular than:

`m_1* m_2=-1`

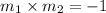
where:

`\begin{gathered} m_1=\text{ first line slope} \\ m_2=\text{ second line slope} \end{gathered}`

line :

`\begin{gathered} y=mx+c \\ y=-5x+1 \end{gathered}`

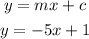
So perpendicular line slope is:

`\begin{gathered} m_1m_2=-1 \\ -5* m_2=-1 \\ m_2=(1)/(5) \end{gathered}`

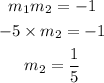
So equation of perpendicular line is:

`\begin{gathered} y=mx+c \\ y=(x)/(5)+c \end{gathered}`

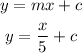
Line pass is (-2,-5)

`\begin{gathered} y=(x)/(5)+c \\ -5=-(2)/(5)+c \\ c=(2)/(5)-5 \\ c=-(23)/(5) \end{gathered}`

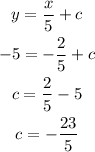
Final equation of perpendicular line is:

`\begin{gathered} y=mx+c \\ y=(x)/(5)-(23)/(5) \end{gathered}`

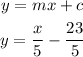
(b) parallel line slope is same for each other line is:

`\begin{gathered} m_1=m_2 \\ m_1=-5 \\ m_2=-5 \end{gathered}`

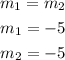
so parallel line equation is:

`\begin{gathered} y=mx+c \\ y=-5x+c \end{gathered}`

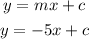
line pass at point (-2,-5) then.

`\begin{gathered} y=-5x+c \\ -5=-5*(-2)+c \\ -5=10+c \\ c=-10-5 \\ c=-15 \end{gathered}`

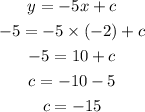
So parallel line equation is:

`\begin{gathered} y=mx+c \\ y=-5x+(-15) \\ y=-5x-15 \end{gathered}`