1 Answer

Ask a Question

Reinhardt · Answer 1 · 2023-12-17T05:59:52+0000

ANSWER:

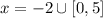
$x=-2\cup\lbrack0,5\rbrack$

Explanation:

We have the following inequality:

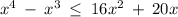
$\: x^4\: -\: x^3\: \le\: 16x^2\: +\: 20x$

We rewrite and solve for x, just like this:

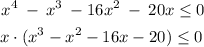
$\begin{gathered} \: x^4\: -\: x^3\: -16x^2\: -\: 20x\le0 \\ x\cdot(x^3-x^2-16x-20)\le0 \end{gathered}$

The resulting factor is calculated by means of the rational root theorem and we would have the following:

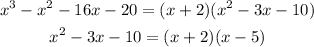
$\begin{gathered} x^3-x^2-16x-20=(x+2)(x^2-3x-10) \\ x^2-3x-10=(x+2)(x-5) \end{gathered}$

Therefore, we replace and finally it would look like this:

$\begin{gathered} x\cdot(x+2)(x+2)(x-5)\le0 \\ x\cdot(x+2)^2\cdot(x-5)\le0 \\ \text{ Therefore:} \\ x=0,x<0,x=-2,x<-2,0If we mix all the values found, we would have:[tex]\begin{gathered} x=-2,0\le x\le5 \\ \text{ The interval notation:} \\ x=-2\cup\lbrack0,5\rbrack \end{gathered}$

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions