Question

List each zero of "f" according to its multiplicity in the categories below.

Answer 1

Okay, here we have this:

We need to find the zeros and it's multiplicity of the following polynomial:

`f(x)=5x(x-4)(x+9)^2(x+3)`

So, considering that in a function of the following form:

`f(x)=a\cdot(x-x_0)^(m_0)(x-x_1)^(m_1)\cdot\ldots\cdot(x-x_n)^(m_n)`

The zeros will be: x₀, x₁, ..., xn

The multiplicities are:

`m_0,^{}m_1,\ldots,\text{ }m_n`

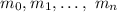
In this case we obtain that the zeros with their respectives multiplicities are:

Zeros of multiplicity one: 0, 4, -3

Zeros of multiplicity two: -9