Question

Write a quadratic equation in intercept form whose graph passes through the points (-6,0)(-4,0) and (-3,3).

Answer 1

We have to write a quadratic equation in intercept form.

The parabola passes throught he points (-6,0), (-4,0) and (-3,3).

The points (-6,0) and (-4,0) are roots of the parabola, so we can start by writing them in factorized form as:

`y=a(x-(-6))(x-(-4))=a(x+6)(x+4)`

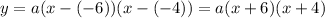
Now, we will use the third point (-3,3) to find the quadratic parameter a by replacing x with -3 and y with 3:

`\begin{gathered} y=a(x+6)(x+4) \\ 3=a(-3+6)(-3+4) \\ 3=a(3)(1) \\ 3=3a \\ a=(3)/(3) \\ a=1 \end{gathered}`

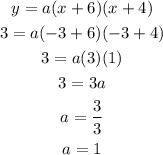
Then, as a = 1, we get the equation:

`y=(x+6)(x+4)`

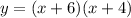
We can expand the factors as:

`\begin{gathered} y=(x+6)(x+4) \\ y=x^2+6x+4x+6\cdot4 \\ y=x^2+10x+24 \end{gathered}`

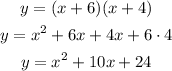
We can check the points by graphing the equation as:

Answer: the equation is y = x² + 10x + 24